LA LATITUDE ET L’HEURE LOCALE
Présentation
La latitude et l’heure locale s’obtinrent par des observations de hauteur. De nombreux instruments furent employés pour mesurer la hauteur ou pour lire directement ces éléments.
Instruments compliqués et d’un usage délicat. Il valait mieux construire des tables, c’est ce que fit Cassini, ou utiliser des graphiques.
Pour lire ce dossier, dans sa version initiale (mise en page de 1931), télécharger le PDF de ce chapitre à ce lien
Le fac-similé dans la version de 1931, est ici
![]()
La mécométrie ne donnait qu’un lieu géométrique du navire : la courbe d’égale déclinaison sur laquelle il se trouvait. Pour le situer complètement il fallait un second élément : la latitude. D’autre part dans les déterminations astronomiques de la longitude la latitude était nécessaire soit pour le calcul des observations, soit pour la détermination de l’heure locale. Or latitude et heure locale s’obtinrent par des observations de hauteur. Il faut donc dire quels furent les instruments employés pour mesurer la hauteur ou pour avoir directement les éléments en question.
![]()
Car il y eut des tentatives pour les obtenir par une observation directe. Cortes avait déjà décrit une machine compliquée pour avoir la latitude et l’heure. Et voici l’ « hémisphère nautique » de Coignet qui date de 1581.
On voit sur la figure 10 qu’il réalisait les cercles principaux de la sphère locale : l’horizon, le méridien, l’équateur, le vertical et le cercle horaire, partiellement, de l’astre, au moins du Soleil. Pour l’utiliser, on orientait le méridien de l’instrument au moyen de la boussole encastrée dans le cercle horizontal : puis, ayant dirigé l’alidade, par les pinnules sur le Soleil, on déplaçait l’équateur et le long de l’équateur, l’élément du cercle de déclinaison de manière à faire affleurer l’extrémité de l’alidade à la division correspondant à la valeur de la déclinaison. On lisait alors la latitude et l’heure. C’était aussi peu pratique que possible. Aussi William Burrough n’aimait-il pas l’instrument, pas plus que le P. Fournier qui pensait qu’il n’avait jamais servi, bien qu’il en ait vu, dit-il, entre les mains de matelots. Néanmoins il était d’une conception ingénieuse et nous avons vu un instrument très moderne construit dans une forme semblable.
Dès lors, en orientant le grand bras vers les Gardes de la Petite Ourse l’index se trouvait dirigé vers le Soleil et donnait l’heure par conséquent. A une distance αC du centre C égal à la distance polaire de α Petite Ourse, l’instrument étant supposé adapté à l’extrémité du « sea quadrant » de Wright (fig. 12 bis), se trouvait le centre α du « cercle de la Polaire » par lequel on obtenait la projection de la distance polaire indiquée sur le méridien, d’où résultait la latitude. On voit ainsi qu’il fallait viser à l’horizon, à la Polaire, aux Gardes et maintenir le « sea quadrant » vertical ; ce qui devait être bien difficile sur un bâtiment à la mer, sinon impossible. Cependant on trouve déjà le nocturnal dans Medina. Mais il comprenait alors simplement un cercle des jours donnant pour le milieu et la fin de chaque mois la position des Gardes à minuit. En mettant le centre du cercle sur la Polaire et un diamètre origine vertical, on voyait si l’on était avant ou après minuit et de combien d’heures ; au moins lorsqu’on n’était pas difficile sur l’exactitude recherchée. D’autre part Nunes prétendait que la distance polaire de α Petite Ourse variait suivant le « climat », c’est-à-dire alors suivant la latitude, et il condamnait le nocturnal.
![]()
Les instruments qui suivent avaient plus de valeur et d’utilité. Nous avons vu l’origine de l’astrolabe. Ce fut parfois un instrument très lourd, jusqu’à peser 10 à 12 livres, afin de mieux résister, disait-on, au vent et à l’agitation du vaisseau.
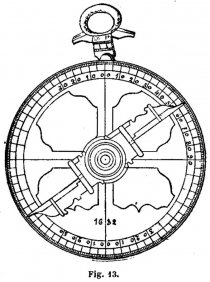 Le musée de Caudebec-en-Caux en possède un daté de 1632 (fig. 13). D’après Anthiaume il a 184 mm. de diamètre et pèse 3.840 grammes. L’observation devait être incommode, même avec deux observateurs, et fatigante.
Le musée de Caudebec-en-Caux en possède un daté de 1632 (fig. 13). D’après Anthiaume il a 184 mm. de diamètre et pèse 3.840 grammes. L’observation devait être incommode, même avec deux observateurs, et fatigante.
Medina s’étend longuement sur l’instrument et il agrémente son exposé d’amusantes figures où l’on voit un homme de mer, fort grossier, observant avec son astrolabe dans tous les cas qui peuvent se produire pour l’observation de la latitude. C’est ainsi qu’un incunable antérieur, conservé à Munich, et destiné aux marins, ne contient pas moins de 17 exemples du même problème. Dans ce Règlement de Munich et dans d’autres traités analogues, où l’on trouve les déclinaisons du Soleil, il semble, d’après Bensaude, qu’on ait extrait ces dernières de l’Almanach Perpetuum dû à un savant juif : Abraham Zacuto, qui enseigna l’astronomie à Salamanque de 1474 à 1492 et qui passa ensuite en Portugal. Il tenait lui même ses connaissances des Arabes donc sans doute des Tables Alphonsines. On observera sur la figure 13 le rapprochement des pinnules que l’on maintenait très peu éloignées l’une de l’autre pour donner plus de stabilité à l’alidade ; mais il n’en était pas toujours ainsi comme l’attestent les figures des traités ; elles se trouvaient aussi aux extrémités de l’alidade, ce qui convenait mieux à une orientation précise. C’est ainsi par exemple qu’est représenté l’astrolabe du traité de Wright.
On simplifia l’astrolabe en le réduisant à un simple anneau sans diamètres intérieurs ni alidade pour en faire l’ anneau astronomique. Il était percé d’une ou deux fenêtres par où le Soleil formait image sur la tranche intérieure opposée. On avait alors des angles inscrits, donc des graduations qui étaient deux fois plus étendues que les graduations correspondantes de l’astrolabe ; de sorte que l’anneau avait plus de sensibilité. Cet anneau fut employé très tard puisque, d’après Montucla Chazelles, ingénieur hydrographe, travaillant aux cartes de la Méditerranée jusqu’aux environs de 1700, on y employa avec assez de succès l’anneau astronomique. Il était d’ailleurs plus commode que l’astrolabe.
Mais l’arbalète ne donnait pas toujours lieu à des histoires « gracieuses » comme celle qui précède. Comme toutes les nouveautés elle eut ses détracteurs ; en particulier chez ces vieux « shipmasters » qui, au dire de Bourne, se moquaient de ceux qui employaient cartes et bâtons de Jacob. Ils appelaient ceux qui observaient avec cet instrument pour obtenir la latitude « sun shooters » ou « star shooters » et demandaient s’ils les attrapaient. On passa outre, comme on l’a vu. L’instrument fut très discuté, il est vrai, à juste titre et en même temps très étudié. Wright nota ses principales imperfections. L’œil n’était pas placé à un point défini à l’extrémité de la flèche ; il y avait excentricité de ce fait et il estime les erreurs qui en résultaient à 10, 20, 30’. Il n’était pas commode, malgré la légèreté de l’instrument, de viser à l’horizon et à l’astre.
![]()
Comme dans toutes les questions relatives à la navigation, le XVIIIe siècle fut ici encore marqué par de nouvelles tentatives pour doter les marins de bons instruments propres à la mesure des hauteurs. Ces instruments firent le sujet du prix de 1729, décerné à Bouguer. Dans la pièce envoyée, il décrit un quart de cercle suspendu par un anneau fixé à un de ses côtés, de manière que l’autre côté soit vertical, et il donne aussi, avec de grands détails, un projet d’anneau astronomique monté sur une boîte lestée flottant sur l’eau d’un récipient. Les dimensions sont les suivantes : l’anneau à 17 à 18 pouces (46 à 49 cm.) de diamètre ; les côtés de la boite qui le soutient ont 24 et 8 pouces (65 et 22 cm.) ; son tirant d’eau est de 2 pouces 1/3 (6 cm.). Il tenait beaucoup à ce que le centre de gravité du système flottant soit exactement entre la flottaison et le fond du flotteur, voulant ainsi atténuer les mouvements de l’anneau ; et il voulait, en se passant de l’horizon, éviter les erreurs dues aux réfractions horizontales et à la dépression, aux anomalies de laquelle on attribuait alors une valeur très grande. L’astronome anglais Wales faisait en effet monter à 10’ les erreurs moyennes sur la dépression pour lesquelles nous comptons aujourd’hui 1 à 2’.
![]()
Toutefois Bouguer donnait la préférence, en fin de compte, au quartier anglais de Davis, dont il proposait seulement de simplifier la construction en donnant la même dimension aux deux arcs et en fixant le verre ardent à une des extrémités de l’arc unique, de 55 à 58 centimètres de rayon, les réunissant.
![]()
Tout cela n’avait pas grande valeur, mais ce mémoire de Bouguer lui fournit l’occasion d’étudier la réfraction atmosphérique dans l’hypothèse de couches sphériques et de donner une théorie correcte de la « solaire », nom qu’il donne à la courbe décrite par un rayon lumineux arrivant d’un astre à un observateur. Il n’était pas, en réalité, comme il le croyait, le premier à avoir tenu compte de la sphéricité des couches dans cette question ; mais il fut bien le premier à aboutir à des formules pratiquement utilisables.
![]()
Le prix de 1745 eut pour sujet « la meilleure manière de trouver l’heure en mer, le jour, au crépuscule et la nuit, surtout quand on ne voit point l’horizon ». Les pièces envoyées étant jugées insuffisantes, le prix fut reproposé pour 1747 et doublé. On le partagea entre Daniel Bernouilli, professeur en médecine à Bâle, qui renvoya, avec un supplément, sa pièce de 1745, et un autre auteur resté anonyme. L’Académie, toutefois, rappelait qu’elle ne déclarait pas adopter toutes les propositions contenues dans les pièces qu’elle couronnait. Bernouilli (pièce de 1745) propose d’abord de rapporter la hauteur à un fanal placé sur esquif : idée impraticable qui a pourtant été reprise par Faye il y à une cinquantaine d’années.
![]()
L’autre pièce envoyée au concours varie ces exercices en déduisant l’angle horaire de la connaissance de l’azimut, de la déclinaison et de la hauteur ou de la latitude ; ou encore de la latitude des déclinaisons et des ascensions droites de deux astres et du temps écoulé entre leurs passages par la même hauteur, ce qu’on exprimait en disant au même almicantarat ; un almicantarat était un petit cercle dont le centre est au zénith. Mais tout cela n’était pas marin. Enfin, on trouve d’autres projets aussi peu satisfaisants, comme celui qui consistait à monter une astrolabe sur une suspension à la cardan, afin de la rendre insensible aux mouvements du navire ; et cet autre, dans lequel on imaginait d’articuler un secteur immense au sommet d’un mât ajouté au navire à cet effet.
![]()
Nous devons au jésuite Pézenas, professeur d’hydrographie de 1728 à 1749, et directeur de l’observatoire de Marseille, un grand nombre d’articles et d’ouvrages sur la longitude. Des études qu’il a publiées dans les Mémoires de Mathématiques, rédigés à l’observatoire de Marseille en 1755, contiennent la description d’instruments destinés à mesurer la hauteur ou à calculer l’angle horaire.
![]()
Hadley enfin, toujours dans le même but de se passer de l’horizon, montait un quart de cercle sur un axe vertical fixé au navire. Pour mesurer l’inclinaison de l’axe au moment où on prenait la hauteur, il adaptait un niveau d’eau au bas du quartier. Ce niveau (fig. 24) était constitué par un tube sans fin formé en haut et en bas de deux arcs concentriques. Le liquide ne remplissait pas l’arc inférieur qui était gradué. Il se déplaçait dans ce tube avec les mouvements du navire, mais un robinet R, fermé au moment où on effectuait une visée, permettait d’arrêter le liquide dans la position qu’il avait à cet instant, et, par suite, d’avoir l’inclinaison de l’instrument. Or cette idée a été récemment reprise en aviation.
On voit qu’on se donnait beaucoup de mal pour n’aboutir qu’à des résultats médiocres. Les niveaux ne pouvaient que courir après leur position d’équilibre sans cesse variable, parce qu’elle dépendait à chaque instant de la verticale apparente et non de la verticale vraie.
- En 1751, l’un de ces inventeurs, l’anglais Serson, fut mieux inspiré en pensant à utiliser le mouvement gyroscopique d’une toupie en rotation rapide, pour conserver à bord la direction de la verticale. Short, dans les Philosophical Transactions de 1751-52, dit que l’instrument de Serson a été perdu à bord du Victory. Il dit aussi que la toupie tournait 35 minutes dans l’air et 2 heures 16 minutes dans le vide. Mais Smeaton améliora cet instrument de Serson, notamment en rapprochant le centre de gravité de la toupie de la pointe de l’axe de rotation. Bouguer décrit cet instrument de Smeaton. C’était une toupie au-dessus de laquelle était fixé un miroir horizontal. Elle était de métal, avait 3 pouces (8 cm.) de diamètre et était très plate, ayant la forme du couvercle d’une boite cylindrique. « Sous le miroir, dit Bouguer, il y a un petit creux en agate qui reçoit l’extrémité d’une pointe d’acier. » Pour lancer le gyroscope, on le fixait au moyen du pivot et d’une barre de bois contre laquelle s’appuyait son axe et qui était liée à la partie supérieure de la boîte contenant l’appareil. Le mouvement de rotation était donné par un ruban enroulé autour de l’axe. Les difficultés étaient de faire la machine et de faire le lancement, l’axe étant vertical. C’était toutefois le germe d’une heureuse idée, puisque, c’est en mettant le point de suspension au-dessus du centre de gravité, que l’amiral Fleuriais a réalisé récemment un précieux appareil, donnant, à un très petit nombre de minutes près, la direction de l’horizon, par une mer moyennement agitée au moins.
- Cette toupie de Smeaton coûtait, d’après Delambre, 3 guinées et elle tournait pendant 12 à 15 minutes. La recherche d’un horizon artificiel donna d’ailleurs lieu à des idées étranges. C’est ainsi que Medina et Fournier après lui, proposaient de remplacer l’horizon invisible par l’extrémité d’une perche d’une hauteur égale à celle de l’œil de l’observateur et tenue verticalement par un aide à quelque distance. La nuit, ajoutait-on, on pouvait éclairer cette extrémité. Robertson, lui, décrit un niveau formé d’une cuvette de mercure sur lequel flottait un miroir de métal ou de verre. Le tout, devant être employé à bord, à la mer, était suspendu à la cardan. Il ajoute que par temps calme, la mer elle-même peut servir d’horizon artificiel en réfléchissant le Soleil ; observant, il est vrai, que ce dernier moyen n’était généralement pas employé. On n’a pas de peine à le croire.
- La hauteur obtenue, il fallait y apporter les corrections nécessaires. Ici intervenaient la dépression de l’horizon, la réfraction, la parallaxe, le demi-diamètre de l’astre quand c’était le Soleil. Nous avons vu que l’idée de la dépression était très nette chez Wright. Il n’en est pas de même, bien plus tard, chez le P. Fournier qui semble la confondre avec une variation de la parallaxe, due à une augmentation du rayon de la Terre égale à l’altitude, et qui conclut qu’elle est négligeable. Il ajoute qu’il dit cela « contre un certain qui a imprimé depuis peu d’années… qu’il faut avoir égard à la hauteur de l’œil qui opère » d’où on voit que les idées les plus élémentaires pour nous ont quelquefois eu de la peine à se faire accepter des esprits les plus prévenus. On pensait aussi que la réfraction n’était pas la même pour le Soleil et la Lune d’une part, pour les étoiles d’autre part. Les tables que donne le P. Fournier attribuent, d’après Tycho Brahé, à l’horizon, une réfraction de 34’ au Soleil et à la Lune ; de 30’ seulement aux étoiles. A 45° elle est de 5" pour les deux premiers astres, puis nulle ; tandis qu’elle devient nulle pour les étoiles à partir de 20°. Et Wright fait exactement de même. D’un autre coté on croyait à la possibilité de réfractions énormes. Ainsi Barentz hivernant à terre par 76° de latitude, au nord de la Nouvelle Zemble, vit le Soleil réapparaitre après la nuit polaire, avec une avance de 15 jours. On disait quelquefois que ce retour prématuré était le fait d’une réfraction de 4°. On ne sait d’ailleurs que penser de cette anomalie qui a beaucoup occupé le monde savant au XVIIe siècle.
Quant à la parallaxe solaire, Fournier la fait, d’après Lansberge, qui l’avait déterminée en mesurant les dimensions de l’ombre de la Terre sur la Lune pendant une éclipse de Lune de 2’18". On sait qu’il a fallu attendre les mesures de 1672 à Paris et Cayenne pour approcher de la vérité, en la fixant alors à 9"5. Enfin le même recueil fait varier le diamètre du Soleil de 29’50" à 34’9" et va, comme Ptolémée, jusqu’à attribuer un diamètre de 36’ à la Lune. Un siècle plus tard environ, ces diverses corrections, telles qu’on les trouve dans Bouguer, sont correctes ; mais par contre la troisième édition du livre de Wright, qui est de 1657, donne encore 3’ à la parallaxe solaire.
D’ailleurs, au dire de Radouay, les pilotes négligeaient toutes ces corrections ; aussi bien que les erreurs systématiques de leurs instruments avec lesquels ils visaient au-dessus ou au dessous de l’horizon, à vue ; comme on fait d’un mauvais fusil en visant à coté du but, ajoutait-il.
Mais dans cette question de la latitude, bien des voies différentes de celles qui précèdent furent tentées. Là aussi on essaya des rapprochements, on imagina des idées qui nous paraissent étranges, lorsque nous ne prenons pas garde, encore une fois, que nous ne cherchons pas autrement. C’est ainsi par exemple que quelques-uns imaginèrent que la latitude était égale en chaque lieu à l’inclinaison de l’aiguille aimantée. Et voici une idée plus singulière, qui prit corps pour un temps, chez certains autres. On la relève chez le P. Fournier. D’après le P. Cabens, dit-il, « les veines, lits ou couches des montagnes escarpées du côté d’orient ou d’occident font avec l’horizon un angle qui précisément est égal à l’élévation du pôle en leur lieu. Il a cela très véritable après l’avoir plusieurs fois observé en Lombardie et dans l’Apennin ; et de même a fait le P. Kircher en Allemagne, Hongrie, France, quantité d’iles et côtes maritimes ».
La question de l’angle horaire fut beaucoup plus longue à résoudre, en dehors des levers et couchers. Le calcul de la formule donnant l’angle horaire par la hauteur, jusqu’au XVIIIe siècle, était hors de portée des navigateurs ; et elle exigeait la connaissance de la latitude et de la déclinaison.
Les méthodes graphiques furent très en honneur. On les croyait plus que les calculs à la portée du commun des navigateurs et suffisamment précises. Lalande, dans son Abrégé de Navigation de 1793 les rappelle. Voici d’abord la méthode qu’on employait d’ordinaire.
![]()
C’est ici le lieu de parler du problème ou plutôt de la solution de Douwes. Ce navigateur hollandais indiqua sa méthode vers 1740 et elle a été connue en Angleterre, sans démonstration, en 1749. Le problème était célèbre au XVIIIe siècle, mais il n’est pas tout à fait celui qu’on a appelé communément de ce nom au XIXe siècle. Il consistait dans la détermination de la latitude par l’observation de deux hauteurs et de l’intervalle de temps qui séparait les observations. C’est que l’angle horaire en 1740, était considéré comme une donnée à laquelle suffisaient les observations simples des levers et couchers ; et il n’était pas question alors d’en conclure la longitude. Il y avait donc à résoudre par rapport à φ le système
- sin h = sin φ sin L + cos φ cos L cos P
- sin h’ = sin φ sin L + cos φ cos L cos (P + I).
On sait la méthode simple qui a été employée depuis la fin du XVIIIe siècle jusqu’au moment du triomphe définitif des lieux géométriques, qui ne remonte guère qu’à une cinquantaine d’années. On calculait l’angle horaire au moyen de la latitude estimée par l’observation la plus éloignée du méridien ; puis la latitude au moyen de l’angle horaire obtenu par l’observation la plus rapprochée du méridien. Bien entendu cette pratique ne s’est pas présentée du premier coup ; elle n’a été acquise que par étapes. La solution de Douwes est la première solution approchée qui ait été proposée. En retranchant membre à membre les équations ci-dessus et employant la latitude estimée, Douwes obtenait d’abord des valeurs approchées P1 et P’1 des angles horaires par
- sin (P1 + I/2) = sin (P’1 – I/2) = cos ((h’ + h)/2) sin ((h’ - h)/2) / ( cos φe cos L sin (I/2) )
puis, par P1 par exemple, il calculait la latitude par - cos (φ1 - L) = sin h + 2 cos φe cos L sin2 (P1 /2)
employant encore φe dans le calcul.
On voit par quel détour singulier il parvenait au résultat. Il avait d’ailleurs publié des tables pour faciliter les calculs et, en 1760, Pemberton fut assez séduit par la méthode pour étudier les limites de son application.
Or, supposons qu’au lieu de φ1 on ait cherché la latitude φ’ par : sin h = sin φ’ sin L + cos φ’ cos L cos P1 , puis, que, prenant φ’ comme latitude estimée, on ait calculé, en supposant les azimuts invariables, une nouvelle latitude φ« à partir de φ’ de la même manière qu’on avait obtenu φ1 en partant de φe et ainsi de suite avec φ », etc. En poursuivant l’opération un nombre suffisant de fois, théoriquement, une infinité de fois, on aurait trouvé une latitude identique à celle de Rossel dans le voyage de Dentrecasteaux, sur lequel nous reviendrons, latitude donnée par :
- φ - φe = m (tg A . tg A’) / (tg A’ – tg A)
où “m” est la différence des angles horaires estimés calculés avec φ1 et A et A’ les azimuts. Et c’est la deuxième étape de la solution, avant la solution classique rappelée plus haut.
On rencontre en fait la solution de Douwes dans tous les traités de Navigation et d’Astronomie de la fin du XVIIIe siècle et du commencement du XIXe et le problème en question est en outre l’objet de très longs développements, en particulier dans Robertson qui examine quantité de cas particuliers, suivant une habitude chère aux écrivains d’autrefois, lesquels ignoraient les solutions générales. La solution rigoureuse par les formules des triangles sphériques était d’ailleurs également indiquée ; par exemple, on la trouve dans une Navigation de Fournier en 1826 ; elle était longue et, quelques années plus tard, Pagel ne craignait pas de dire qu’elle n’était jamais employée. Près d’un siècle auparavant Bouguer ne jugeait pas autrement ce problème. Il est pourtant encore résolu rigoureusement en 1868 dans Caillet : Traité de Navigation.
![]()
Pour éviter l’emploi des tables de logarithmes, on utilisa, aussitôt qu’elles furent inventées, les échelles logarithmiques de Gunter, sur lesquelles étaient tracés les logarithmes des nombres, des sinus et des tangentes. On en trouva communément, gravées sur buis ou ivoire, dès l’invention des logarithmes par Napier, en 1614. En 1765, un sieur Baradelle les grava sur cuivre « avec des soins qu’on ne peut attendre que des artistes qui savent porter la précision et la finesse des divisions à un point qu’il serait difficile d’exprimer ». La règle de Baradelle avait deux pieds (64 cm.) de longueur.
![]()
Il valait mieux construire des tables. C’est ce que fit Cassini, qui calcula 24 pages de tables, insérées dans sa relation du voyage de l’Enjouée. Les hauteurs y variaient de 5 en 5° ; les latitudes, de degré en degré, de 34 à 51° et les déclinaisons, de degré en degré également entre ±23°29’. Il n’y donne pas de parties proportionnelles et il fallait attendre que la hauteur ait atteint une des valeurs de la table pour pouvoir s’en servir. Lalande, à la fin du siècle, fit beaucoup mieux. Dans ses tables, la déclinaison varie de degré en degré, de – 24° à + 24°. La latitude va de 2° en 2° jusqu’à 40° ; puis de degré en degré jusqu’à 60°. Les hauteurs sont comprises entre 0 et 48° à l’équateur, entre 0 et 30° à la latitude de 60°. Il y a des parties proportionnelles pour les variations de la déclinaison, de la hauteur et de la latitude. Elles furent calculées en grande partie par sa nièce, Mme Lefrançais, aussi habile à manier l’aiguille que prompte à aider son oncle dans ses calculs. Citons enfin les graphiques par lesquels Margetts figura de semblables tables. Ils donnaient très simplement l’angle horaire en ne nécessitant que l’usage d’un compas.
![]()
Pour terminer, ajoutons que la méthode des hauteurs correspondantes à la mer était également signalée. Bouguer, qui l’a employée en allant en Amérique, en parle dans son Traité de Navigation et la Connaissance des Temps donnait, depuis le début du siècle, une table des corrections nécessaires par suite de la variation de la déclinaison du Soleil. Elle est également exposée dans Robertson, qui indique que l’on peut observer à 3, 4, 5 heures de part et d’autre du méridien et qu’il n’y a pas à se préoccuper de la variation de la déclinaison du Soleil si l’on est à plus de « six semaines ou deux mois » des équinoxes.
![]()
![]()


 Suivi RSS
Suivi RSS Conception
Conception


 Version imprimable
Version imprimable Publié Novembre 2014, (màj Février 2015) par :
Publié Novembre 2014, (màj Février 2015) par :

























